April 22, 2017

なんで 0.99999... = 1 なの？

昔、疑問に思っていた事を、ふと思い出した。

0.99999... = 1

これは本当だろうか？ 正しい気もした、間違っているきもした。

1 / 3 = 0.33333...
0.33333... x 3 = 0.99999...
1 / 3 x 3 = 1
よって、0.99999... = 1 は正しい

0.9 < 1
0.99 < 1
0.999 < 1
このように、0.9 の後にどれだけ 9 を付け足しても 1 より小さい
よって、0.99999... < 1
よって、0.99999... = 1 は間違い

どちらの考え方も一見正しいように見えるが、正反対の結論になってしまった。

実は、この議論を始めるために最初に確認しなくてはいけない事がある。 0.99999... とは何だう？

0.9 の後に 9 を無限個、続けた数字？ 「無限」って整数だったの？ 整数って事は、偶数か奇数のどちらかだ。 「無限」って偶数？奇数？

「無限」について数学的に正しく扱う事は簡単ではない。 だが、ここが上の議論で一番重要な点だ。 0.33333... や 0.99999... を正しく定義できれば、このパラドックスは理解できる。

「無限」という言葉を使うと難しくなるので、その言葉を使わずに 0.99999... を定義してみよう。 以下のような数列 a_n を考える。

• a₁ = 0.9

• a₂ = 0.99

• a₃ = 0.999

• ...

ちなみに、数学的に厳密に書くと

• a₁ = 0.9

• a_k+1 = a_k + (9/10)^k+1

となる。 （まあ、表現が難しくなっただけで今回の記事には関係無いが）

さて、この数列 a_n は以下の 2 個の特徴をもつ。

1. どんな自然数 n においても、a_n < 10

2. どんな自然数 n においても、a_n < a_n+1

1 と 2 を真面目に証明するとこの記事が長くなりすぎるので、ここは「当たり前」で許してほしい。

では、1 と 2 の条件を満たす数列のグラフはどんな形になるだろう？ (今は a_n の詳しい事は一回忘れて、「1 と 2 の条件を満たす数列」のグラフを考えよう。)

例えばこんな形になるのではないか？

上図を見ると直観的に分かるかもしれないが、a_n は「n を大きくするとある数に近づく」という性質を持っている。

なぜなら「2 どんな自然数 n においても、a_n < a_n+1 」より、a_n は、n を大きくすると

• 際限なく大きくなる

• 上限となる、ある数に近づく

のどちらかである。

そして、 「際限なく大きくなる」「1 どんな自然数 n においても、a_n < 10」 と明らかに矛盾する。

この「上限となる、ある数 x」を先ほどの図に加えるとこのようになる。

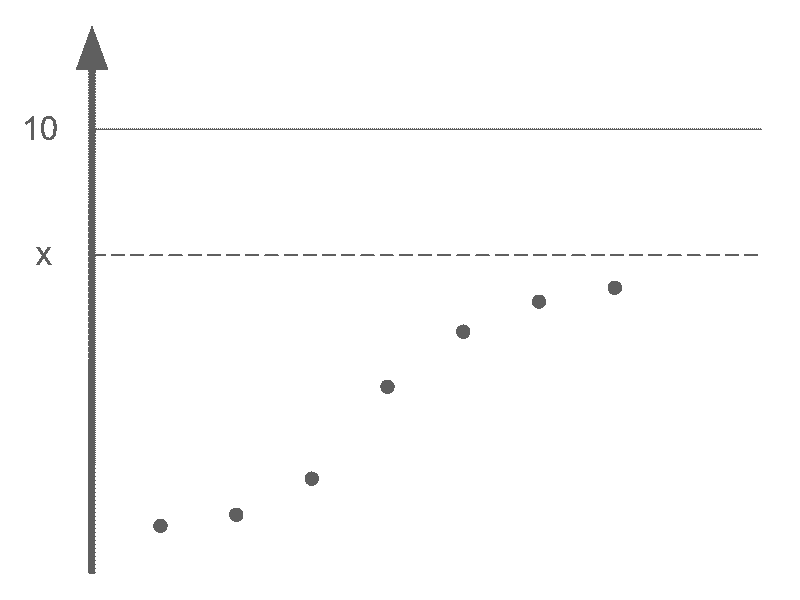
では、この x について厳密な定義をしてみよう。 （「n を大きくすると近づく数」という表現は数学的には曖昧すぎる）

先ほど a_n について「1 どんな自然数 n においても、a_n < 10」と書いた。

当たり前だが、この条件はもっと厳しくする事ができる。 例えば、

• どんな自然数 n においても、a_n < 5

• どんな自然数 n においても、a_n < 3

これはどちらも正しい。

この条件を一番厳しくした時の値で x を定義する。（10, 5, 3 という数字を使ったが、もっと小さい数を使う事も出来る。） この使用可能な数の中で、最小値を x とするのだ。

正確に書くと以下のようになる。

a) どんな自然数 n においても、a_n < k を満たす数 k は 2 個以上存在する。x はそのような k の中の最小値。

別の言い方をすると、こんな風になるかもしれない。

b) どんな自然数 n においても、a_n < x。ただし、y < x を満たす全ての数 y において、 y < a_n となる n をが 1 個以上存在する。

x の定義は上記の a), b) どちらでもよい。

数学的にはいい加減だが少しだけ直観的な表現にすると、

c) x とは 0.9 の後に 9 を多く続けた数より、少しだけ大きい数（「多く」とは、100万でも 10億でも良い。）

とも言えるだろう。 「少しだけ大きい」という部分がポイントだ。

そして、この数 x を 0.99999... と名付けよう。

すると、「0.99999... = 1」とは、a) の表現を用いると「0.9 の後に 9 をいくつ続けた数よりも大きい数は 2 個以上存在する。そのような数の最小値は 1 である。」

b) の表現を用いると「0.9 の後に 9 をいくつ続けても 1 より小さい。1 より小さい全ての数 y について、0.9 の後に 9 をいくつか続けると y より大きくなる事がある。」

c) の表現を用いると「0.9 の後に 9 を多く続けた数より、少しだけ大きい数は 1 である。」

という事になる。

どうだろう。

"0.9 の後に 9 を無限個繋げた数" = 1

という表現とは全然違う印象を受けるのではないか？

では、最初のパラドックスに戻ってみよう。 長くなるので、以下では c) の表現のみを用いてみる。

1 / 3 = 0.33333...
(1 / 3 = "0.3 の後に 3 を多く続けた数より、少しだけ大きい数")
0.33333... x 3 = 0.99999...
("0.3 の後に 3 を多く続けた数より少し大きい数" x 3 = "0.9 の後に 9 を多く続けた数より少し大きい数")
1 / 3 x 3 = 1
よって、0.99999... = 1 は正しい
("0.9 の後に 9 を多く続けた数より少し大きい数" = 1 は正しい。)

これは全て正しい。

1 / 3 = "0.3 の後に 3 を多く続けた数より、少しだけ大きい数"

ここが直観に反するかもしれないが、実際には正しい。 （数学的に厳密な証明は、今回は控える）

0.9 < 1
0.99 < 1
0.999 < 1
このように、0.9 の後にどれだけ 9 を付け足しても 1 より小さい。
よって、0.99999... < 1
("0.9 の後に 9 を多く続けた数より少し大きい数" < 1）
よって、0.99999... = 1 は間違い。
("0.9 の後に 9 を多く続けた数より少し大きい数" = 1 は間違い)

これは間違っている。

0.9 の後にどれだけ 9 を付け足しても 1 より小さい

"0.9 の後に 9 を多く続けた数より少し大きい数" < 1

この間に議論の飛躍がある。 ここで間違えているのだ。

この疑問を始めて感じたのは、小学生の時だったと思う。 その際、周りの大人たちに聞いたが納得のいく解答は得られなかった。 （今にして思うと、大人にも良く分からなかったのかもしれない）

小学生だったころの自分にも分かるような説明を考えてみたが、どうだろうか。