May 24, 2016

単位が違う値は計算できるの？

知り合いの高校生と物理話していたら、途中で面白い質問が出た。

「単位の違う物を計算して良いんですか？」

一瞬、質問の意図が分からなかったので聞いてみると、学校の先生が「単位が違う物は計算できない」と言っていたとの事。 う〜ん、先生が本気でそんな事言うとは思えないんだけどな。 彼女が先生の言ったことの意味を勘違いしたか、先生が語弊のある言い方をしたのか。

正解をいうと、「単位の違う値同士の足し算、引き算はできない」、「単位の違う値同士の掛け算、割り算はできる」というのが正しい。

簡単な例から考えてみよう。当たり前からスタートして難しい例にたどり着くのは物事を理解する良い方法だ。

5 m の棒と 2 m の棒を考える。

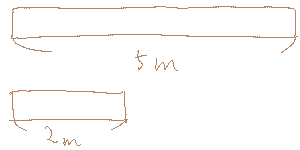
両方とも単位は同じなので、足し算、引き算、掛け算、割り算何でもできるのだが、ここでは例として足し算と掛け算だけ考えよう。

(1): 5 (m) x 2 (m) = 10 (m x m)

(2): 5 (m) + 2 (m) = 7 (m)

1. の式では、後の事を考えて m ² と書かずにあえて m x m と書いてみた。

計算のイメージとしては、例えばこんな感じだろう。

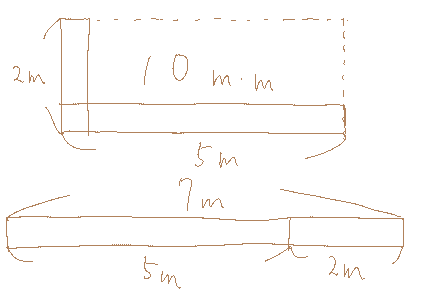
さて、では上記の例で単位を変えてみよう。

具体的には、2 m を 200 cm にしてみる。

掛け算は

(1'): 5 (m) x 200 (cm) = 1000 (m x cm)

今、1 cm = 1/100 m なので、

1000 (m x cm) = 1000 (m x 1/100 m) = 1000 x 1/100 (m x m)

これを (1') と合わせると、

(1''): 5 (m) x 200 (cm) = 10 (m x m)

となり、(1) と同じ値になった。短い方の棒を 2 m と考えても 200 cm と考えても同じ値が出る。 ここまでは、当たり前の事が当たり前にできる事の確認だ。

では、足し算はどうだろう？ 5 m と 200 cm を無理やり足し算してみる。

(2'): 5 (m) + 200 (cm) = 205 (m + cm) --- ???

う〜ん、無理やり計算してみると、おかしな値が出てきてしまった。

5 m の棒と 200 cm の棒を足し算すると 7 m になるはずだ。 しかし、1 cm = 1/100 m という関係式をどう使っても 205 という数字から 7 という数字を導出できそうにない。

厳密な説明ではないが、単位の違う値の掛け算はできるが割り算は出来ない事が直感的に分かるだろう。

と、ここまで書いて思ったのだが、俺自身も単位の違う値の足し算が何で出来ないのか厳密な説明って知らない。高校生相手に偉そうな事言いながら、俺もまだまだだなと思った今日このごろ。